![d = sqrt[ (x-m)^T * S^-1 * (x-m)]](malanobis.png)
The Fisher iris data, sometimes referred to as the Anderson's iris dataset, is a standard dataset provided to statistics and machine learning students. ( for a full description see the Wiki page: Iris flower data set) I first encountered this data set in 1993 during a graduate level neural network class at NC A&T SU.
Recently, I built a clustering algorithm for multi-dimensional datasets. I used the Mahalanobis distance as my similarity metric.
The Mahalanobis distance is defined as:
![d = sqrt[ (x-m)^T * S^-1 * (x-m)]](malanobis.png)
for the purpose of a clustering metric the square root is computational overhead. If f(x) is monotonic increasing then so is sqrt[ f(x) ].
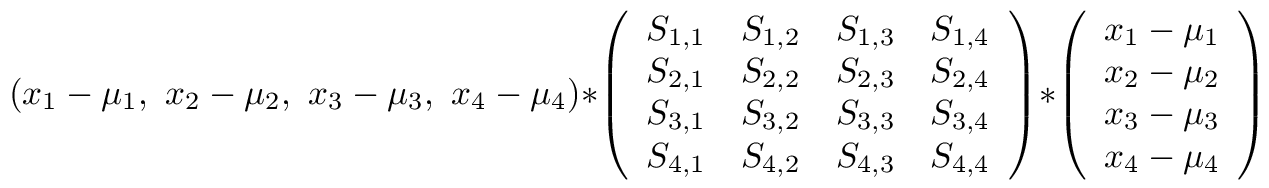
There are three classes in the Iris data: Setosas, Vericolor, and Virginica. Three clusters are created. Each cluster maintains a mean vector and an inverse Covariance matrix. Each sample is compared to each of the three clusters using the Mahalanobis distance metric. The smallest distance value determines which cluster the sample belongs to.
The example below will classify 147 out of 150 samples correctly ( 98 percent )
The inverse Covariance matrices shown below are symmetric so only the lower triangle is shown. The three clusters are defined as:
Mean = 5.006 3.428 1.462 0.246
Inv Covariance =
18.943439
-12.404826 15.570540
-4.500207 1.111079 38.776204
-4.776127 -2.104098 -17.935035 106.045906
Mean = 5.936 2.770 4.260 1.326
Inv Covariance =
9.502764
-3.676217 19.710966
-8.631712 2.116022 19.803758
6.454503 -19.480325 -26.937227 87.244794
Mean = 6.588 2.974 5.552 2.026
Inv Covariance =
10.533867
-3.479726 15.875442
-9.960146 1.102689 13.405821
1.788152 -8.472851 -2.890918 19.314050
Full statistics for combined labeled and unlabeled
|
|
||||||||||||||||||||||||||||
| Spread sheet analysis |
|
Example Source Code |
|